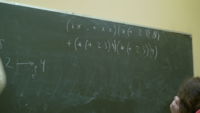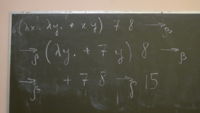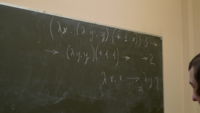Парадигмы программирования, 06 лекция (от 29 октября)
Материал из eSyr's wiki.

[править] лямбда-исчисления
Лямбда-исчисление было придумано Чёрчем задолго до программирования.
Похоже на то, что любую функцию, которая за конечное время даёт результат от конечного числа аргументов, записать можно. Также для неё можно сделать МТ, и т. д.
Лямбда-вычисления это математическая абстракция, некий формализм, прямого отношения к программированию не имеющая
Есть легенда, что когда МакКарти писал лисп, он вдохновился л-исчислением, и лисп писался как его реализация. Это не так, хотя впоследствии лямбда туда была добавлена.
Как в л-исчислислении записывается функция:
λ x . и дальше выражение, задающее функцию. Есть разные способы, обычно используют польскую нотацию
λ x . * 3 x
как это прочитать:
- λ — "функция от"
- . — которая возвращает
Большинство авторов рассматривают ф-цию от одного параметра, но мощности это не уменьшает. Да, некоторые авторы пишут
λ x y z . + x * y z
Но большинство всё же пишут
λ x . λ y . λ z . + x * y z
Такая конструкция называется лямбда-абстракцией, то, что после точки — телом. Как видно, в теле может содержаться произвольное л-выражение, в том числе лямбда.
Если мы видим два лямбда-выражения, E_1 E_2, то это обычно значит, что первое выр. — функция,второе - знач, к которому ее нужно применить.
Чисто синтаксически, функцию всегда применяют к самому левому аргументу. Если есть такая запись:
(...((λ x_1 . λ x_2 . ... λ x_n . E) a_1) a_2) ...) a_n
...то есть соглашение, что такое выражение можно записать несколько короче:
(λ x_1 . lamda x_2 . ... λ x_n . E) a_1 a_2 ... a_n
Более формально можно записать в виде БНФ:
<exp> ::= λ <id> . <exp> | <id> | <exp> <exp> | (<exp>) | <const> <id> ::= идентификатор (какие могут быть идентификаторы --- зависит от того, какой стиль приняли) <const> ::= константы
Константы заслуживают более внимательного рассмотрения. Они могут обозначать:
- Числа. Числа могут быть как целые, так и веществ. Когда рассматривают л-вычисления, обычно до веществ. чисел не доходят.
- Булевы значения: Истина и Ложь. Как конкретно их обозначить, это тоже вопрос философский.
- [ Строки ]. Далеко не все авторы про них вспоминают
- Пустой список. Обычно его обозн. <>, хотя можно обозн. как угодно.
- Функции
- * . + - ....
- Знаки отношений: < > = != >= ...
- Функции работы со списками: CONS, HEAD, TAIL, NULL (предикат, проверка на пустой список)
- Иногда некоторые авторы, в частности, Филд и Харрисон, считают необходимым ввод кортежей. TUPLE-n, INDEX
- COND
- ...
Вообще, можно делать лямбда-вычисления без констант, сконстр. их из первич. понятий, но это к прогр. мало отношения имеет. Без них тяжело. Сначала вводятся списки, потом числа как списки разной длины, а чтобы ввести умножение, нужно несколько страниц исписать.
Примеры лямбда-выражений. Самое простое — просто константа.
42 (+ 6) ; функция, которая прибавляет 6 λ y . * 2 y ; лямбда-абстракция
В многоточие входит в том числе cond. Он аналогичен лисповскому if. Похоже на сишную тернарную операцию.
(λ f . lmbda a λ b . f a b) (λ x . (λ y . x))
Вернёт a ((λ x . (λ y . x)) как ф-ция от двух. арг подст. в f, и сама по себе возвращает первый арг.).
λ f . λ x . COND (= x 1) x (* x (f (- x 1)))
Имеет отношение к вычислению факториала. Вообще, без имён функций тяжело, дальше мы посмотрим, как это решить.
Как л-выр. вычисл. Т.н. правила редукции.
- Константы редуцуются в себя
- Функция и арг. Применяется дельта-правило. Например: + 1 2 →δ 3. Из этого выр. по дельта-правилу, или, применив дельта-редукцию, получаем 3. Понятно, что дельта-правила есть для каждой функции. Например, у нас есть выр.
* (+ 1 2) (- 4 1) →δ * (+ 1 2) 3 →δ * 3 3 →δ 9
- Применение ф-ции, написанной через лямбда-абстракцию. Заменяем чисто текстуально, результат замены --- результат выражения:
(λ x . * x x) 2 →β * 2 2 →δ 4 (λ x . + x x) (* (+ 2 3) 4) →β + (* (+ 2 3) 4) (* (+ 2 3) 4)
- Текстуально оно становится длиннее, но мы избавляемся от символа лямбда.
(λ x . λ y . + x y) 7 8 →β (λ y . + 7 y) 8 →β + 7 8 →δ 15
Редуцируемая часть выражения называется редексом (redex, reducible expression)
Если редексов в выражении нет, тогда говорят, что выражение имеет норм. форму.
Имеется некий подводный камень, связанный с одноименными символами. Рассмотрим выражение:
λ x . (λ x . x) (+ 1 x)
В чём здесь неприятность? Очевидно, что
λ x_2 . (λ λ x_1 . x_1) (+ 1 x_1)
Если взять это в скобки и где-то применить, то понятно, что получится не то, что хотели. Получается конфликт имён. Как это разрешить? Например, постановить, что если мы подобные вещи применяем к чему-то, то внутри ничего не трогать.
Есть второй вариант, т.н. альфа-преобразование. Оно не называется редукцией, поскольку ничего не упрощает, оно переименовывает перемененную.
Если не учитывать контекст имён, то что получится:
(λ x . (λ x . x) (+ 1 x)) 3 -> (λ x . 3) (+ 1 3) -> 7 (λ x . (λ y . y) (+ 1 x)) 3 -> (λ y . y) (+ 1 3) -> ... -> 8
То есть вот, конфликты имён бывают, конфликты имён разрешает альфа-преобразование, это не совсем редекс, хотя записывается также:
λ x. x →α λ y . y
Порядок выбора редексов для редукции. В л-выр может быть несколько редексов, и вопрос, с какого начать? Вопрос интересный и весьма принципиальный. Рассмотрим пример:
(λ f . λ x . f 4 x) (λ y . λ x . + x y) 3 ->
-------- ---------------------------
----------------------------------------------------------
(λ x . (λ y . λ x + x y) 4 x) 3 ->
---- ----
на самом деле, тут в обоих случаях получится одно и то же
1. (λ y . λ x + x y) 4 3 -> (λ x . + x 4) 3 -> + 3 4 -> 7 2. (λ x . (λ x . + x 4) x) 3 -> (λ x . + x 4) 3 -> + 3 4 -> 7
Теорема Чёрча-Россера: если у лямбда-выражения есть нормальная форма, то она единственна (если несколько, то они эквивалентны с точностью до альфа-преобразования).
Из этого следует, что она даже достигается. Но выбрав нехороший порядок редукции, можно не прийти к норм. форме вообще. Есть классический пример, когда один порядок не приводит к норм. форме вообще никогда, другой же за один шаг.
(λ x . λ y . y) ((λ z . z z) (λ z . z. z))
Здесь есть два варианта:
(λ x . λ y . y) ((λ z . z z) (λ z . z. z))
- ------------------------------------
тогда мы достигаем результат за один шаг:
λ y . y
но есть и второй редекс:
(λ x . λ y . y) ((λ z . z z) (λ z . z. z))
----------------------------------
но он при применении даст сам себя:
(λ x . λ y . y) ((λ z . z z) (λ z . z. z))
Вопрос, какой же редекс тогда надо выбирать и зачем? Введём несколько определений.
* Самый левый редекс --- его лямбда или имя примитивной функции находятся текстуально левее всех остальных. * Самый внешний редекс --- тот, который текстуально не содержится ни в каком другом. * Самый внутренний --- тот, в котором не содержится никакой другой.
Есть два порядка?
* Аппликативный --- выбирается самый левый внутренний. * Нормальный --- из всех самых внешних, выбираем самый левый.
Здесь мы сначала применили сначала нормальный, потом аппликативный. Теперь можно уточнить:
Следствие из теор. Чёрча-Россера. нормальный порядок редукции приводит к нормальной форме за конечное число шагов, если она вообще есть.
Теперь самое интересное. Если отвлечься от л-выражений и вернуться к программированию, то можно вспомнить, что есть энергичная и ленивая стратегия вычислений При энергичной мы вычисляем всё, что только можем. При ленивых вычислениях увидев выражение мы запоминаем его и не вычисляем до тех пор, пока не припрёт. Например:
( ) > 3
Вот тут нам действительно надо вычислить значение выражение, не раньше. Бывает ли такое в языках программирования? Бывает, но очень редко. Ленивая семантика из компилир. языков --- только haskell, но все привычные, императивные --- энергичные.
Где можно встретить ленивую модель вычислений? Например, при подстановке макросов. Макропроцессору это просто, поскольку он работает на уровне текстовых строк. В некоторых командно-скриптовых языках ленивая семантика имеется.
Но сейчас, когда мы смотрим на л-выч., мы видим, что ленивый порядок вычисл. оказался в каком-то виде мощнее.
Введём такую вещь, как понятие связанных и свободных переменных
λ x . x y
Понятно, что x связанная, а y --- свободная. Если чуть строже, то построим мн-во FV(E) (free variables(expression)). Как оно вводится:
- FV(x) = {x}
- FV(c) = ∅
- FV(E_1, E_2) = FV(E_1) ∪ FV(e_2)
- FV(λ x . E_1) = FV(E_1) \ {x}
Аналогично можно ввести мн-во Bound variables, BV(E):
- BV(x) = ∅
- BV(c) = ∅
- BV(E_1, E_2) = BV(E_1) ∪ BV(e_2) ; отсюда следует, что прееменная может быт ьи свободная, и связана, но свободна в одной части, а связана в другой
- BV(λ x . E_1) = BV(E_1) ∪ {x}
Выражение, в котором нет связ. переменных, наз. замкнутым. Замкнутыми выр. ещё наз. комбинаторами.
Если x ∉ FV(E), то можно вести речь об η-преобразовании.
Можно заметить, что λ x . E x есть то же самое, что E. Попробуем и то, и другое к a:
E a (λ x . E x) a →β E a
Главное, чтобы в E не было свободной переменной x, иначе ничего не выйдет. Соответственно, делаем это преобразование:
E →η λ x. E x
Что оно позволяет делать? Например, частичное применение встроенных функций. Например, если есть * x y. Является ли * 3 л-выр? Да. А как же с ним работать? Применим η-преобр, получим λ x . * 3 x. Благодаря этому мы можем делать частичное применение функций.
... это называется карринг, по имени учёного Карри Хаскелла (Curry).
Наконец, последнее на сегодня, что же такое Y-combinator. Хочется нам, к примеру, сделать рек. функцию, но как, здесь же нет имён? Мы эту фнкцию получим в кач. второго аргумента. То есть функция получает на фход аргмент и самого себя, и исхитримся и подадим её на вход.
Рассмотрим более идиотический пример --- сумма от 1 до n.
Лектор напишет её сначала на лиспе:
(setq f #'(λ (s x) (if (= x 0) 0 (+ x (funcall s s (- x 1))))))
Что теперь сделать? Нао её вызвать, подав ей на вход число и её саму. Как это сделать?
(funcall f f 5) => 15
можно то же самое сделать и на лямбда-абстракциях
λ s . λ x . COND (= x 0) 0 (+ x (s (- x 1)))
Сущ. неподв. точка, т. е. f(x) = x, и она есть для кажого лямбда-выр.
Есть Y-combinator, который делает:
Y f = f(Y f)
Как выглядит Y-combinator:
Y = λ h . (λ x . h (x x)) (λ x . h (x x))
теперь осталось что?
Y λ s . λ x . COND (= x 0) 0 (+ x (s (- x 1)))
И отредуцировать. Результатом будет функция, от одного арг., выч. сумму.
y-comb. используется в haskell.
Введение в парадигмы программирования
01 02 03 04 05 06 07 08 09 10 11
Календарь
Сентябрь
| 24 | ||||
Октябрь
| 01 | 08 | 15 | 22 | 29 |
Ноябрь
| 05 | 12 | 19 | 26 | |
Декабрь
| 03 |
Экзамен по курсу пройдёт 10 декабря 2009 года в 18:00 в аудитории 524. | Список экзаменационных вопросов