Конструирование Компиляторов, Алгоритмы решения задач
Материал из eSyr's wiki.
(ДКА, допускающий дополнение языка) |
(→Построение приведённого автомата) |
||
| Строка 344: | Строка 344: | ||
Приводим автомат. Удаляем сначала [[Конструирование_Компиляторов%2C_Определения#Непорождающий символ|непорождающие]] (бесплодные, «мёртвые»), '''затем''' [[Конструирование_Компиляторов%2C_Определения#Недостижимый символ|недостижимые]] состояния (определения даны для символов, но очевидным образом переносятся на состояния автомата). | Приводим автомат. Удаляем сначала [[Конструирование_Компиляторов%2C_Определения#Непорождающий символ|непорождающие]] (бесплодные, «мёртвые»), '''затем''' [[Конструирование_Компиляторов%2C_Определения#Недостижимый символ|недостижимые]] состояния (определения даны для символов, но очевидным образом переносятся на состояния автомата). | ||
| + | |||
| + | Вообще говоря, удаление мертвых состояний превращает ДКА в НКА, поскольку в ДКА все переходы должны быть определены. Однако в Dragon Book такое отклонение от формального определения считается всё же допустимым<ref>Aho, Sethi, Ullman, Compilers: Principles, Techniques, and Tools, Addison-Wesley. "3.9.6 Minimizing the Number of States of a DFA"</ref>. | ||
=== Пример === | === Пример === | ||
Версия 09:58, 28 июня 2013
Алгоритмы решения задач в pdf файле
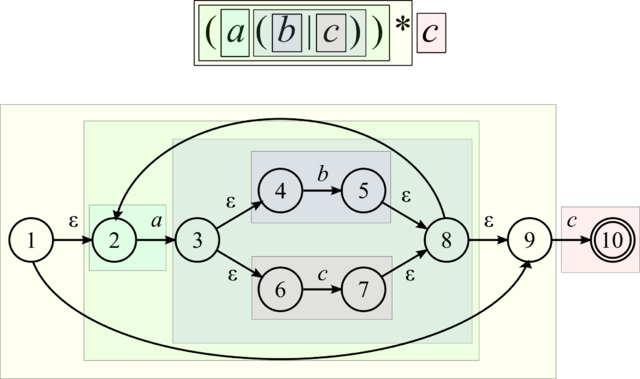
Построение НКА по РВ
Автомат для выражения строится композицией автоматов, соответствующих подвыражениям. На каждом этапе ∃! заключительное состояние, и нет переходов из заключительного состояния и в начальное. Для построения НКА используются следующие преобразования (M(s) и M(t) ниже обозначают соответственно автоматы, соответствующие регулярным выражениям s и t; i и f — некоторые номера состояний НКА):
| подвыражение РВ | автомат |
|---|---|
| ε | |
| a, a ∈ T | |
| s|t | 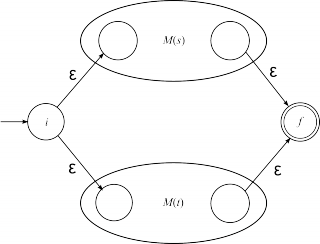
|
| st | 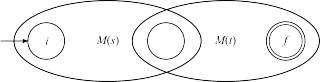
|
| s* | 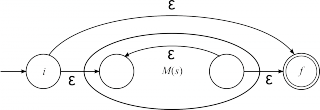
|
Пример
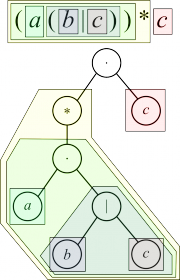
Обычно конечный автомат строится из регулярного выражения, начиная с внутренних символов. То есть, сначала строятся переходы по b и c, потом образуется конструкция b|c, добавляется a, строится автомат для итерации (a(b|c))* и в конце добавляется c.
Построение ДКА по НКА
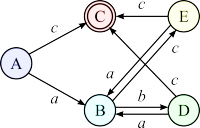
Необходимо по недетерминированному конечному автомату M = (Q, T, D, q0, F) построить детерминированный конечный автомат M = (Q', T, D', q'0, F'). Начальным состоянием для строящегося автомата является ε-замыкание начального состояния автомата исходного. ε-замыкание — множество состояний, которые достижимы из данного путём переходов по ε. Далее, пока есть состояния, для которых не построены переходы (переходы делаются по символам, переходы по которым есть в исходном автомате), для каждого символа вычисляется ε-замыкание множества состояний, которые достижимы из рассматриваемого состояния путём перехода по рассматриваемому символу. Если состояние, которое соответствует найденному множеству, уже есть, то добавляется переход туда. Если нет, то добавляется новое полученное состояние.
Пример
Инициализация
Помечаются состояния, соответствующие ε-замыканию начального. Эти состояния будут соответствовать состоянию A будущего ДКА.
| Состояние ДКА | Множество состояний НКА | Символы, по которым осуществляется переход | ||
|---|---|---|---|---|
| a | b | c | ||
| A | {1, 2, 9} | — | — | — |
Первая итерация
Из ε-замыкания есть переходы в состояния НКА 3 и 10 (по a и c, соответственно). Для состояния 3 ε-замыканием является множество состояний {3, 4, 6}, для состояния 10 — {10}. Обозначим соответствующие данным множествам новые состояния ДКА как B и C.
| Состояние ДКА | Множество состояний НКА | Символы, по которым осуществляется переход | ||
|---|---|---|---|---|
| a | b | c | ||
| A | {1, 2, 9} | B | — | C |
| B | {3, 4, 6} | — | — | — |
| C | {10} | — | — | — |
Вторая итерация
Из множества состояний НКА {3, 4, 6}, соответствующего состоянию ДКА B есть два перехода — в состояние 5 (по b) и 7 (по c). Их ε-замыкания пересекаются, но сами множества различны, поэтому им ставятся в соответствие два новых состояния ДКА — D и E. Из состояний НКА, соответствующих состоянию ДКА C, никаких переходов нет.
| Состояние ДКА | Множество состояний НКА | Символы, по которым осуществляется переход | ||
|---|---|---|---|---|
| a | b | c | ||
| A | {1, 2, 9} | B | — | C |
| B | {3, 4, 6} | — | D | E |
| C | {10} | — | — | — |
| D | {2, 5, 8, 9} | — | — | — |
| E | {2, 7, 8, 9} | — | — | — |
Третья итерация
Из множеств состояний НКА, соответствующих состояниям ДКА D и E переходы делаются в множества состояний, соответствующие уже имеющимся состояниям (из множества {2, 5, 8, 9}, соответствующего состоянию D, по a переход в состояние 3, принадлежащее множеству {3, 4, 6}, соответствующему состоянию ДКА B, по c — переход в состояние 10, соответствующее состоянию C; аналогично для множества, соответствующего состоянию ДКА E). Процесс построения таблицы состояний и переходов ДКА завершён.
| Состояние ДКА | Множество состояний НКА | Символы, по которым осуществляется переход | ||
|---|---|---|---|---|
| a | b | c | ||
| A | {1, 2, 9} | B | — | C |
| B | {3, 4, 6} | — | D | E |
| C | {10} | — | — | — |
| D | {2, 5, 8, 9} | B | — | C |
| E | {2, 7, 8, 9} | B | — | C |
Результат:
Построение праволинейной грамматики по конечному автомату
Каждому состоянию ставим в соответствие нетерминал. Если есть переход из состояния X в состояние Y по а, добавляем правило X → aY. Для конечных состояний добавляем правила X → ε. Для ε-переходов — X → Y.
Пример 1 (детерминированный конечный автомат)
- A → aB | cC
- B → bD | cE
- C → ε
- D → aB | cC
- E → aB | cC
Пример 2 (недетерминированный конечный автомат)
- 1 → 2 | 9
- 2 → a3
- 3 → 4 | 6
- 4 → b5
- 5 → 8
- 6 → c7
- 7 → 8
- 8 → 2 | 9
- 9 → c10
- 10 → ε
Построение ДКА по РВ
Пусть есть регулярное выражение r. По данному регулярному выражению необходимо построить детерминированный конечный автомат D такой, что L(D) = L(r).
Модификация регулярного выражения
Добавим к нему символ, означающий конец РВ — «#». В результате получим регулярное выражение (r)#.
Построение дерева
Представим регулярное выражение в виде дерева, листья которого — терминальные символы, а внутренние вершины — операции конкатенации «.», объединения «∪» и итерации «*». Каждому листу дерева (кроме ε-листьев) припишем уникальный номер и ссылаться на него будем, с одной стороны, как на позицию в дереве и, с другой стороны, как на позицию символа, соответствующего листу.
Вычисление функций nullable, firstpos, lastpos
Теперь, обходя дерево T снизу вверх слева-направо, вычислим три функции: nullable, firstpos, и lastpos. Функции nullable, firstpos и lastpos определены на узлах дерева. Значением всех функций, кроме nullable, является множество позиций. Функция firstpos(n) для каждого узла n синтаксического дерева регулярного выражения дает множество позиций, которые соответствуют первым символам в подцепочках, генерируемых подвыражением с вершиной в n. Аналогично, lastpos(n) дает множество позиций, которым соответствуют последние символы в подцепочках, генерируемых подвыражениями с вершиной n. Для узлов n, поддеревья которых (т. е. дерево, у которого узел n является корнем) могут породить пустое слово, определим nullable(n) = true, а для остальных узлов false. Таблица для вычисления nullable, firstpos, lastpos:
| узел n | nullable(n) | firstpos(n) | lastpos(n) |
|---|---|---|---|
| ε | true | ∅ | ∅ |
| i ≠ ε | false | {i} | {i} |
| u ∪ v | nullable(u) or nullable(v) | firstpos(u) ∪ firstpos(v) | lastpos(u) ∪ lastpos(v) |
| u . v | nullable(u) and nullable(v) | if nullable(u) then firstpos(u) ∪ firstpos(v) else firstpos(u) | if nullable(v) then lastpos(u) ∪ lastpos(v) else lastpos(v) |
| v* | true | firstpos(v) | lastpos(v) |
Построение followpos
Функция followpos вычисляется через nullable, firstpos и lastpos. Функция followpos определена на множестве позиций. Значением followpos является множество позиций. Если i — позиция, то followpos(i) есть множество позиций j таких, что существует некоторая строка ...cd..., входящая в язык, описываемый РВ, такая, что i соответствует этому вхождению c, а j — вхождению d. Функция followpos может быть вычислена также за один обход дерева по следующим двум правилам
- Пусть n — внутренний узел с операцией «.» (конкатенация); a, b — его потомки. Тогда для каждой позиции i, входящей в lastpos(a), добавляем к множеству значений followpos(i) множество firstpos(b).
- Пусть n — внутренний узел с операцией «*» (итерация), a — его потомок. Тогда для каждой позиции i, входящей в lastpos(a), добавляем к множеству значений followpos(i) множество firstpos(а).
Пример
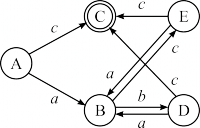
Вычислить значение функции followpos для регулярного выражения (a(b|c))*c.
| Позиция | Значение followpos |
|---|---|
| 1: (a(b|c))*c | {2, 3} |
| 2: (a(b|c))*c | {1, 4} |
| 3: (a(b|c))*c | {1, 4} |
| 4: (a(b|c))*c | {5} |
Построение ДКА
ДКА представляет собой множество состояний и множество переходов между ними. Состояние ДКА представляет собой множество позиций. Построение ДКА заключается в постепенном добавлении к нему необходимых состояний и построении переходов для них. Изначально имеется одно состояние, firstpos(root) (root — корень дерева), у которого не построены переходы. Переход осуществляется по символам из регулярного выражения. Каждому символу соответствует множество позиций {pi}. Объединение всех followpos(x) есть состояние в которое необходимо перейти, где x — позиция, присутствующая как среди позиций состояния и так и среди позиций символа из РВ, по которому осуществляется переход. Если такого состояния нет, то его необходимо добавить. Процесс нужно повторять, пока не будут построены все переходы для всех состояний. Конечными объявляются все состояния, содержащие позицию добавленного в конец РВ символа #.
Пример
Построить ДКА по регулярному выражению (a(b|c))*c.
| Состояние ДКА | Символ | ||
|---|---|---|---|
| a {1} | b {2} | c {3, 4} | |
| A {1, 4} | B {2, 3} | — | C {5} |
| B {2, 3} | — | A {1, 4} | A {1, 4} |
| C {5} | — | — | — |
Построение ДКА с минимальным количеством состояний
ДКА с минимальным числом состояний строится для всюду определённого ДКА, т.е. такого, что 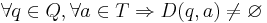 . Для любого ДКА существует эквивалентный ему всюду определённый ДКА.
. Для любого ДКА существует эквивалентный ему всюду определённый ДКА.
Построение всюду определённого ДКА
Введём новое состояние 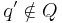 и определим новое множество состояний
и определим новое множество состояний 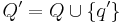 .
.
Определим новую функцию перехода так:
-
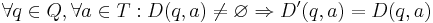 .
.
-
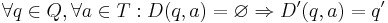 .
.
-
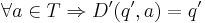 .
.
Построение разбиения (формально)
Построим начальное разбиение П множества состояний на две группы: заключительные состояния F и остальные S\F, т. е. П = {F, Q\F}.
Применить к каждой группе G ∈ П следующую процедуру. Разбить G на подгруппы так, чтобы состояния s и t из G оказались в одной группе тогда и только тогда, когда для каждого входного символа a состояния s и t имеют переходы по a в состояния из одной и той же группы в П.
Полученные подгруппы добавляем в новое разбиение Пnew.
Принимаем П = Пnew и повторяем построение разбиения до стабилизации, т. е. пока разбиение не перестанет меняться.
Построение разбиения (алгоритм)
Для построения разбиения существует следующий алгоритм. Строим таблицу переходов для исходного автомата, строим начальное разбиение.
Каждой группе из разбиения назначаем идентификатор (для начального разбиения, например, 0 и 1).
Каждому состоянию (каждой строке таблицы) приписываем строку вида “a.bcd…xyz”, где [a, b, …, z] — идентификатор группы, к которой принадледжит состояние из [первого столбца (откуда переходим), второго столбца (куда переходим по первому символу), …, последнего столбца (куда переходим по последнему символу)].
Строим новые группы по совпадению строк, т. е. так, чтобы в одну группу попали состояния с одинаковыми приписанными строками.
Затем, новая итерация. Назначаем получившимся группам новые идентификаторы, например {0, 1, …, n}. И повторяем построение разбиения до стабилизации.
Заметим, что когда в группе осталось одно состояние, на последующих этапах построения разбиения можно уже не выписывать строку идентификаторов для этого состояния, т. к. эта строка в любом случае будет уникальна за счёт первого символа строки. Иначе говоря, при разбиении с группой из одного состояния ничего не случится — она переносится в новое разбиение как есть.
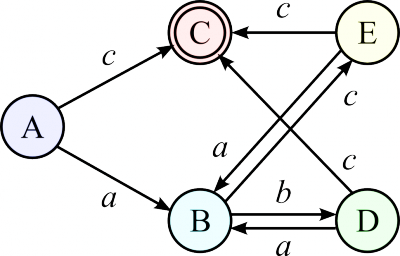
Построение приведённого автомата
Каждая из получившихся групп становится состоянием нового ДКА. Если группа содержит начальное (заключительное) состояние исходного автомата, эта группа становится начальным (соответственно заключительным) состоянием нового ДКА. Переходы строятся очевидным образом: переход в состояние из группы считается переходом в группу.
Приводим автомат. Удаляем сначала непорождающие (бесплодные, «мёртвые»), затем недостижимые состояния (определения даны для символов, но очевидным образом переносятся на состояния автомата).
Вообще говоря, удаление мертвых состояний превращает ДКА в НКА, поскольку в ДКА все переходы должны быть определены. Однако в Dragon Book такое отклонение от формального определения считается всё же допустимым[1].
Пример
Для построим ДКА с минимальным числом состояния для ДКА следующего вида:
- Начальное разбиение: {C} (конечное состояние), {A, B, D, E} (все остальные состояния).
- {C} (без изменений), {A, D, E}, {B}, (так как из A, D, E по a, c переходим в B и C соответственно).
- Больше никаких разбиений сделать не можем.
Пусть группе {C} соответствует состояние С, группе {A, D, E} — состояние A, а группе {B} — состояние B. Тогда получаем ДКА с минимальным числом состояний:
Пример (алгоритм построения разбиения)
Таблица переходов для всюду определённого (добавлено состояние Z) ДКА, соответствующего РВ (ab|ε)a*|abb|b*a. Из заданий экзамена 2012 года.
| a | b | I0 | I1 | |
|---|---|---|---|---|
| →A* | B | C | 0.01 | 0.12 |
| B* | D | E | 0.00 | 1.01 |
| C | F | C | 1.01 | |
| D* | D | Z | 0.01 | 0.04 |
| E* | D | Z | 0.00 | 1.03 |
| F* | Z | Z | 0.11 | |
| Z | Z | Z | 1.11 |
Итерации:
- I0: ABCDEF(0), CZ(1).
- I1: AD(0), BE(1), C(2), F(3), Z(4).
- I2: A, B, C, D, E, F, Z.
Результат: в автомате и так было минимальное число состояний :-)
ДКА, допускающий дополнение языка
Алгоритм построения ДКА, принимающего дополнение языка L (L̅) состоит из двух шагов:
- Построение полного ДКА
- Построение из него искомого автомата
На самом деле, нет такого понятия, как полный ДКА. Под полным ДКА некоторые преподаватели понимают автомат, в таблице переходов которого нет пустых клеток. Однако в соответствии с определением ДКА — δ: Q × Σ → Q — такого быть не может. Такой автомат, впрочем, удовлетворяет определению НКА. Тем не менее, в ходе решения нередко получается именно такой НКА, которому до ДКА не хватает лишь переходов.
Для того, чтобы его пополнить, достаточно добавить новое состояние X, и "вместо" несуществующих переходов добавить переходы в это новое состояние. При этом нужно не забыть добавить переходы из X в X. Легко заметить, что там, где исходный автомат не принимал некоторую цепочку ввиду отсутствия перехода, новый автомат будет переходить в состояние X и "зацикливаться" в нём. Поскольку новое состояние не является принимающим (финальным), новый автомат также не будет принимать эту цепочку.
Теперь для того, чтобы построить искомый автомат, требуется лишь поменять роли принимающих и непринимающих состояний. Иными словами, F' = Q \ F.
Построение LL(k) анализатора
Преобразование грамматики
Не всякая грамматика является LL(k)-анализируемой. Контекстно-свободная грамматика принадлежит классу LL(1), если в ней нет конфликтов типа FIRST-FIRST (левая рекурсия — частный случай такого конфликта) и FIRST-FOLLOW.
Иногда удаётся преобразовать не LL(1)-грамматики так, чтобы они стали LL(1). Некоторые (точнее, те, которые рассматривались в курсе) преобразования приведены ниже.
Удаление левой рекурсии
Пусть у нас имеется правило вида (здесь и далее в этом разделе, заглавные буквы — нетерминальные символы, строчные — цепочки любых символов):
- A → Aa | Ab | … | Ak | m | n | … | z
Оно не поддается однозначному анализу, поэтому его следует преобразовать.
Легко показать, что это правило эквивалентно следующей паре правил:
- A → mB | nB | … | zB
- B → aB | bB | … | kB | ε
Левая факторизация
Суть данной процедуры — устранение неоднозначности в выборе правил по левому символу. Для этого находится общий левый префикс и то, что за ним может следует выносится в новое правило (строчные буквы — цепочки любых символов)
Пример
- A → ac | adf | adg | b
Преобразуется в
- A → aB | b
- B → c | df | dg
Что в свою очередь превратится в
- A → aB | b
- B → c | dС
- С → f | g
Пример преобразования грамматики
G = {{S, A, B}, {a, b, c}, P, S}
P:
- S → SAbB | a
- A → ab | aa | ε
- B → c | ε
Удаление левой рекурсии для S:
- S → aS1
- S1 → AbBS1 | ε
Левая факторизация для A:
- A → aA1 | ε
- A1 → b | a
Итоговая грамматика:
- S → aS1
- S1 → AbBS1 | ε
- A → aA1 | ε
- A1 → b | a
- B → c | ε
Построение FIRST и FOLLOW
FIRST(α), где α ∈ (N ∪ T)* — множество терминалов, с которых может начинаться α. Если α ⇒ ε, то ε ∈ FIRST(α). Соответственно, значение функции FOLLOW(A) для нетерминала A — множество терминалов, которые могут появиться непосредственно после A в какой-либо сентенциальной форме. Если A может являться самым правым символом в некоторой сентенциальной форме, то заключительный маркер $ также принадлежит FOLLOW(A)
Вычисление FIRST
Для терминалов
- Для любого терминала x, x ∈ T, FIRST(x) = {x}
Для нетерминалов
- Если X — нетерминал, то положим FIRST(X) = {∅}
- Если в грамматике есть правило X → ε, то добавим ε к FIRST(X)
- Для каждого нетерминала X и для каждого правила вывода X → Y1…Yk добавим в FIRST(X) множества FIRST всех символов в правой части правила до первого, из которого не выводится ε, включая его
Для цепочек
- Для цепочки символов X1…Xk FIRST есть объединение FIRST входящих в цепочку символов до первого, у которого ε ∉ FIRST, включая его.
Пример
Посчитать FIRST для всех нетерминалов и правил вывода грамматики:
- S → aS1
- S1 → AbBS1 | ε
- A → aA1 | ε
- A1 → b | a
- B → c | ε
FIRST нетерминалов в порядке разрешения зависимостей:
- FIRST(S) = {a}
- FIRST(A) = {a, ε}
- FIRST(A1) = {b, a}
- FIRST(B) = {c, ε}
- FIRST(S1) = {a, b, ε}
FIRST для правил вывода:
- FIRST(aS1) = {a}
- FIRST(AbBS1) = {a, b}
- FIRST(ε) = {ε}
- FIRST(aA1) = {a}
- FIRST(a) = {a}
- FIRST(b) = {b}
- FIRST(c) = {c}
Вычисление FOLLOW
Вычисление функции FOLLOW для символа X:
- Пусть FOLLOW(X) = {∅}
- Если X — аксиома грамматики, то добавить в FOLLOW маркер $
- Для всех правил вида A → αXβ добавить FIRST(β)\{ε} к FOLLOW(X) (за X могут следовать те символы, с которых начинается β)
- Для всех правил вида A → αX и A → αXβ, ε ∈ FIRST(β) добавить FOLLOW(A) к FOLLOW(X) (то есть, за X могут следовать все символы, которые могут следовать за A, в случае, если в правиле вывода символ X может оказаться крайним правым)
- Повторять предыдущие два пункта, пока возможно добавление символов в множество
Пример
Посчитать FOLLOW для всех нетерминалов грамматики:
- S → aS1
- S1 → AbBS1 | ε
- A → aA1 | ε
- A1 → b | a
- B → c | ε
Результат:
- FOLLOW(S) = {$}
- FOLLOW(S1) = {$} (S1 — крайний правый символ в правиле S → aS1)
- FOLLOW(A) = {b} (после A в правиле S1 → AbBS1 следует b)
- FOLLOW(A1) = {b} (A1 — крайний правый символ в правиле A → aA1, следовательно, добавляем FOLLOW(A) к FOLLOW(A1))
- FOLLOW(B) = {a, b, $} (добавляем FIRST(S1)\{ε} (следует из правила S1 → AbBS1), FOLLOW(S1) (так как есть S1 → ε))
Составление таблицы
В таблице M для пары нетерминал-терминал (в ячейке M[A, a]) указывается правило, по которому необходимо выполнять свёртку входного слова. Заполняется таблица следующим образом: для каждого правила вывода заданной грамматики A → α (где под α понимается цепочка в правой части правила) выполняются следующие действия:
- Для каждого терминала a ∈ FIRST(α) добавить правило A → α к M[A, a]
- Если ε ∈ FIRST(α), то для каждого b ∈ FOLLOW(A) добавить A → α к M[A, b]
- ε ∈ FIRST(α) и $ ∈ FOLLOW(A), добавить A → α к M[A, $]
- Все пустые ячейки — ошибка во входном слове
Пример
Построить таблицу для грамматики
- S → aS1
- S1 → AbBS1 | ε
- A → aA1 | ε
- A1 → b | a
- B → c | ε
Результат:
| a | b | c | $ | |
|---|---|---|---|---|
| S | S → aS1 (Первое правило, вывод S → aS1, a ∈ FIRST(aS1)) | Error (Четвёртое правило) | Error (Четвёртое правило) | Error (Четвёртое правило) |
| S1 | S1 → AbBS1 (Первое правило, вывод S1 → AbBS1, a ∈ FIRST(AbBS1)) | S1 → AbBS1 (Первое правило, вывод S1 → AbBS1, b ∈ FIRST(AbBS1)) | Error (Четвёртое правило) | S1 → ε (Третье правило, вывод S1 → ε, ε ∈ FIRST(ε), $ ∈ FOLLOW(S1)) |
| A | A → aA1 (Первое правило, вывод A → aA1, a ∈ FIRST(aA1)) | A → ε (Второе правило, вывод A1 → ε, b ∈ FOLLOW(A1)) | Error (Четвёртое правило) | Error (Четвёртое правило) |
| A1 | A1 → a (Первое правило, вывод A1 → a, a ∈ FIRST(a)) | A1 → b (Первое правило, вывод A1 → b, b ∈ FIRST(b)) | Error (Четвёртое правило) | Error (Четвёртое правило) |
| B | B → ε (Второе правило, вывод B → ε, a ∈ FOLLOW(B)) | B → ε (Второе правило, вывод B → ε, a ∈ FOLLOW(B)) | B → c (Первое правило, вывод B → c, c ∈ FIRST(c)) | B → ε (Третье правило, вывод B → ε, $ ∈ FOLLOW(B)) |
Разбор строки
Процесс разбора строки довольно прост. Его суть в следующем: на каждом шаге считывается верхний символ v из стека анализатора и берется крайний символ c входной цепочки.
- Если v - терминальный символ
- Если v совпадает с с, то они оба уничтожаются, происходит сдвиг
- Если v не совпадает с с, то сигнализируется ошибка разбора
- Если v - нетерминальный символ, c возвращается в начало строки, вместо v в стек возвращается правая часть правила, которое берется из ячейки таблицы M[v, c]
Процесс заканчивается, когда и строка и стек дошли до концевого маркера (#).
Пример
разберем строку «aabbaabcb»:
| стек | строка | действие |
|---|---|---|
| S# | aabbaabcb$ | S → aS1 |
| aS1# | aabbaabcb$ | сдвиг |
| S1# | abbaabcb$ | S1 → AbBS1 |
| AbBS1# | abbaabcb$ | A → aA1 |
| aA1bBS1# | abbaabcb$ | сдвиг |
| A1bBS1# | bbaabcb$ | A1 → b |
| bbBS1# | bbaabcb$ | сдвиг |
| bBS1# | baabcb$ | сдвиг |
| BS1# | aabcb$ | B → ε |
| S1# | aabcb$ | S1 → AbBS1 |
| AbBS1# | aabcb$ | A → aA1 |
| AbBS1# | aabcb$ | A → aA1 |
| aA1bBS1# | aabcb$ | сдвиг |
| A1bBS1# | abcb$ | A1 → a |
| abBS1# | abcb$ | сдвиг |
| bBS1# | bcb$ | сдвиг |
| BS1# | cb$ | B → c |
| cS1# | cb$ | сдвиг |
| S1# | b$ | S1 → AbBS1 |
| AbBS1# | b$ | A → ε |
| bBS1# | b$ | сдвиг |
| BS1# | $ | B → ε |
| S1# | $ | S1 → ε |
| # | $ | готово |
Построение LR(k) анализатора
Вычисление k в LR(k)
Не существует алгоритма, который позволял бы в общем случае для произвольной грамматики вычислить k. Обычно, стоит попробовать построить LR(1)-анализатор. Если у него на каждое множество приходится не более одной операции (Shift, Reduce или Accept), то грамматика LR(0). Если же при построении LR(1)-анализатора возникает конфликт и коллизия, то данная грамматика не является LR(1) и стоит попробовать построить LR(2). Если не удаётся построить и её, то LR(3) и так далее.
Пополнение грамматики
Добавим новое правило S' → S, и сделаем S' аксиомой грамматики. Это дополнительное правило требуется для определения момента завершения работы анализатора и допуска входной цепочки. Допуск имеет место тогда и только тогда, когда возможно осуществить свёртку по правилу S → S'.
Построение канонической системы множеств допустимых LR(1)-ситуаций
В начале имеется множество I0 с конфигурацией анализатора S' → .S, $. Далее к этой конфигурации применяется операция закрытия до тех пор, пока в результате её применения не перестанут добавляться новые конфигурации. Далее, строятся переходы в новые множества путём сдвига точки на один символ вправо (переходы делаются по тому символу, который стоял после точки до перехода и перед ней после перехода), и в эти множества добавляются те конфигурации, которые были получены из имеющихся данным образом. Для них также применяется операция закрытия, и весь процесс повторяется, пока не перестанут появляться новые множества.
Пример
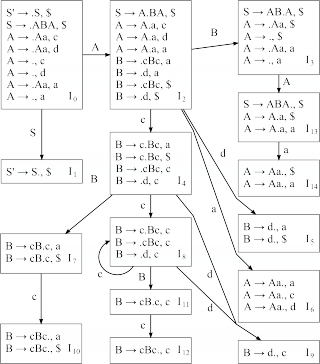
Построить каноническую систему множеств допустимых LR(1)-ситуаций для указанной грамматики:
- S' → S
- S → ABA
- A → Aa | ε
- B → cBc | d
Решение:
- Строим замыкание для конфигурации S' → .S, $:
- S → .ABA, $
- Для полученных конфигураций (S → .ABA, $) также строим замыкание:
- A → .Aa, c
- A → .Aa, d
- A → ., c
- A → ., d
- Для полученных конфигураций (A → .Aa, c; A → .Aa, d) также строим замыкание:
- A → .Aa, a
- A → ., a
- Больше конфигураций в состоянии I0 построить нельзя — замыкание построено
- Из I0 можно сделать переходы по S и A и получить множество конфигураций I1 и I2, состоящее из следующих элементов:
- I1 = {S' → S., $}
- I2 = {S → A.BA, $; A → A.a, c; A → A.a, d; A → A.a, a}
- I1 не требует замыкания
- Построим замыкание I2:
- B → .cBc, a
- B → .cBc, $
- B → .d, a
- B → .d, $
- Аналогично строятся все остальные множества.
Построение таблицы анализатора
Заключительным этапом построения LR(1)-анализатора является построение таблиц Action и Goto. Таблица Action строится для символов входной строки, то есть для терминалов и маркера конца строки $, таблица Goto строится для символов грамматики, то есть для терминалов и нетерминалов.
Построение таблицы Goto
Таблица Goto показывает, в какое состояние надо перейти при встрече очередного символа грамматики. Поэтому, если в канонической системе множеств есть переход из Ii в Ij по символу A, то в Goto(Ii, A) мы ставим состояние Ij. После заполнения таблицы полагаем, что во всех пустых ячейках Goto(Ii, A) = Error
Построение таблицы Actions
- Если есть переход по терминалу a из состояния Ii в состояние Ij, то Action(Ii, a) = Shift(Ij)
- Если A ≠ S' и есть конфигруация A → α., a, то Action(Ii, a) = Reduce(A → α)
- Для состояния Ii, в котором есть конфигурация S' → S., $, Action(Ii, $) = Accept
- Для всех пустых ячеек Action(Ii, a) = Error
Пример
Построить таблицы Action и Goto для грамматики
- S' → S
- S → ABA
- A → Aa | ε
- B → cBc | d
Решение:
| Action | Goto | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | c | d | $ | S | S' | A | B | a | c | d | |
| I0 | Reduce(A → ε) | Reduce(A → ε) | Reduce(A → ε) | I1 | I2 | ||||||
| I1 | Accept | ||||||||||
| I2 | Shift(I6) | Shift(I4) | Shift(I5) | I3 | I6 | I4 | I5 | ||||
| I3 | Reduce(A → ε) | Reduce(A → ε) | I13 | ||||||||
| I4 | Shift(I8) | Shift(I9) | I7 | I8 | I9 | ||||||
| I5 | Reduce(B → d) | Reduce(B → d) | |||||||||
| I6 | Reduce(A → Aa) | Reduce(A → Aa) | Reduce(A → Aa) | ||||||||
| I7 | Shift(I10) | I10 | |||||||||
| I8 | Shift(I8) | Shift(I9) | I11 | I8 | I9 | ||||||
| I9 | Reduce(B → d) | ||||||||||
| I10 | Reduce(B → cBc) | Reduce(B → cBc) | |||||||||
| I11 | Shift(I12) | I12 | |||||||||
| I12 | Reduce(B → cBc) | ||||||||||
| I13 | Shift(I14) | Reduce(S → ABA) | I14 | ||||||||
| I14 | Reduce(A → Aa) | Reduce(A → Aa) | |||||||||
Разбор цепочки
На каждом шаге считывается верхний символ v из стека анализатора и берется крайний символ c входной цепочки.
Если в таблице дейстивий на пересечении v и c находится:
- Shift(Ik), то в стек кладется с и затем Ik. При этом c удаляется из строки.
- Reduce(A → u), то из верхушки стека вычищаются все терминальные и нетерминальные символы, составляющие цепочку u, после чего смотрится состояние Im, оставшееся на верхушке. По таблице переходов на пересечении Im и A находится следующее состояние Is. После чего в стек кладется A, а затем Is. Строка остается без измененеий.
- Accept, то разбор закончен
- пустота - ошибка
Пример
Построим разбор строки aaaccdcc:
| Стек | Строка | Действие |
| I0 | aaaccdcc$ | Reduce(A → ε), goto I2 |
| I0 A I2 | aaaccdcc$ | Shift(I6) |
| I0 A I2 a I6 | aaccdcc$ | Reduce(A → Aa), goto I2 |
| I0 A I2 | aaccdcc$ | Shift(I6) |
| I0 A I2 a I6 | accdcc$ | Reduce(A → Aa), goto I2 |
| I0 A I2 | accdcc$ | Shift(I6) |
| I0 A I2 a I6 | ccdcc$ | Reduce(A → Aa), goto I2 |
| I0 A I2 | ccdcc$ | Shift(I4) |
| I0 A I2 c I4 | cdcc$ | Shift(I8) |
| I0 A I2 c I4 c I8 | dcc$ | Shift(I9) |
| I0 A I2 c I4 c I8 d I9 | cc$ | Reduce(B → d), goto I11 |
| I0 A I2 c I4 c I8 B I11 | cc$ | Shift(I12) |
| I0 A I2 c I4 c I8 B I11 c I12 | c$ | Reduce(B → cBc), goto I7 |
| I0 A I2 c I4 B I7 | c$ | Shift(I10) |
| I0 A I2 c I4 B I7 c I10 | $ | Reduce(B → cBc), goto I3 |
| I0 A I2 B I3 | $ | Reduce(A → ε), goto I13 |
| I0 A I2 B I3 A I13 | $ | Reduce(S → ABA), goto I1 |
| I0 S I1 | $ | Accept |
Трансляция арифметических выражений (алгоритм Сети-Ульмана)
Примечание. Код генерируется doggy style Motorola-like, то есть
Op Arg1, Arg2
обозначает
Arg2 = Arg1 Op Arg2
Построение дерева
Дерево строится как обычно для арифметического выражения: В корне операция с наименьшим приоритетом, далее следуют операции с приоритетом чуть выше и так далее. Скобки имеют наивысший приоритет. Если имеется несколько операций с одинаковым приоритетом — a op b op c, то дерево строится как для выражения (a op b) op с.
Пример
Построить дерево для выражения a + b / (d + a − b × c / d − e) + c × d
Решение: Запишем выражение в виде
((a) + ((b) / ((((d) + (a)) − ((b) × (c)) / (d)) − (e)))) + ((c) × (d))
Тогда в корне каждого поддерева будет операция, а выражения в скобках слева и справа от неё — её поддеревьями. Например, для подвыражения ((b) × (c)) / (d) в корне соответствующего поддерева будет операция «/», а её поддеревьями будут являться подвыражения ((b) × (c)) и (d).
Разметка дерева (вычисление количества регистров)
Далее необходимо вычислить для каждого поддерева, сколько регистров потребуется для его вычисления. Делается это разметкой дерева снизу вверх по следующим правилам:
- Если вершина — левый лист (то есть, переменная), то помечаем её нулём.
- Если вершина — правый лист, то помечаем её единицей
- Если мы разметили для некоторой вершины оба её поддерева, то её размечаем следующим образом:
- Если левое и правое поддеревья помечены разными числами, то выбираем наибольшее из них
- Если левое и правое поддеревья помечены одинаковыми числами, то данному поддереву сопоставляем число, на единицу большее того, которым помечены поддеревья
| Разметка листьев | Разметка дерева с одинаковыми поддеревьями | Левое поддерево помечено большим числом | Правое поддерево помечено большим числом |
|---|---|---|---|
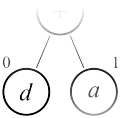
| 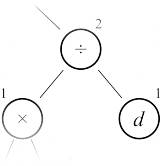
| 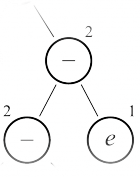
| 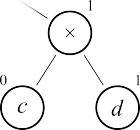
|
Пример
Разметить дерево, построенное для выражения a + b / (d + a − b × c / d − e) + c × d
Распределение регистров и генерация кода
Распределение регистров происходит следующим образом:
- Корню назначается R0
- Если метка левого потомка меньше или равна метке правого, то левому потомку назначается регистр на единицу больший, чем предку, а правому — такой же, как и предку.
- Если метка левого потомка больше метки правого, то правому потомку назначается регистр на единицу больший, чем предку, а левому — такой же, как и предку.
Формируется код путём обхода дерева снизу вверх следующим образом:
1. Для вершины с меткой 0 код не генерируется
2. Если вершина — лист X с меткой 1 и регистром Ri, то ему сопоставляется код
MOVE X, Ri
3. Если вершина внутренняя c регистром Ri и её левый потомок — лист X с меткой 0, то ей соответствует код
<Код правого поддерева> Op X, Ri
4. Если поддеревья вершины с регистром Ri — не листья и метка правой вершины больше или равна метке левой (у которой регистр Rj, j = i + 1), то вершине соответствует код
<Код правого поддерева> <Код левого поддерева> Op Rj, Ri
5. Если поддеревья вершины с регистром Ri — не листья и метка правой вершины (у которой регистр Rj, j = i + 1) меньше метки левой, то вершине соответствует код
<Код левого поддерева> <Код правого поддерева> Op Ri, Rj MOVE Rj, Ri
При этом нельзя сразу сделать Op Rj, Ri так как Op в общем случае некоммутативна. В случае, если Op коммутативна, делать Op Rj, Ri вместо Op Ri, Rj; MOVE Rj, Ri можно всё равно нельзя.
Общее правило: выписывать код снизу вверх сначала для вершины с большей меткой, потом с меньшей (если метки равны, то сначала для правой).
Пример
Распределить регистры и сгенерировать код для выражения a + b / (d + a − b × c / d − e) + c × d
Решение:
Распределение регистров показано на графике справа. Сгенерированный код:
MOVE d, R0 ;R0 = d MOVE c, R1 ;R1 = c MUL b, R1 ;R1 = (b × c) DIV R1, R0 ;R0 = (b × c) / d MOVE a, R1 ;R1 = a ADD d, R1 ;R1 = a + d SUB R1, R0 ;R0 = (a + d) − ((b × c) / d) MOVE e, R1 ;R1 = e SUB R0, R1 ;R1 = ((a + d) − ((b × c) / d)) − e MOVE R1, R0;R0 = ((a + d) − ((b × c) / d)) − e DIV b, R0 ;R0 = b / (((a + d) − ((b × c) / d)) − e) ADD a, R0 ;R0 = a + (b / (((a + d) − ((b × c) / d)) − e)) MOVE d, R1 ;R1 = d MUL c, R1 ;R1 = c × d ADD R0, R1 ;R1 = (a + (b / (((a + d) − ((b × c) / d)) − e))) + (c × d) MOVE R1, R0;R0 = (a + (b / (((a + d) − ((b × c) / d)) − e))) + (c × d)
Трансляция логических выражений
В данном разделе показан способ генерации кода для ленивого вычисления логических выражений. В результате работы алгоритма получается кусок кода, который с помощью операций TST, BNE, BEQ вычисляет логическое выражение путём перехода на одну из меток: TRUELAB или FALSELAB.
Построение дерева
Дерево логического выражения отражает порядок его вычисления в соответствии с приоритетом операций, то есть, для вычисления значения некоего узла дерева (который есть операция от двух операндов, являющимися поддеревьями узла) мы должны сначала вычислить значения его поддеревьев.
Приоритет операций: наивысший приоритет у операции NOT, далее идёт AND, а затем OR. Если в выражении используются другие логические операции то они должны быть выражены через эти три определённым образом (обычно, других операций нет и преобразования выражения не требуется). Ассоциативность у операций одного приоритета — слева направо, то есть A and B and C рассматривается как (A and B) and C
Пример
Построить дерево для логического выражения not A or B and C and (B or not C).
Решение: см. схему справа.
Разметка дерева
Для каждой вершины дерева вычисляются 4 атрибута:
- Номер узла
- Метка, куда необходимо перейти, если выражение в узле — истина (true label, tl)
- Метка, куда необходимо перейти, если выражение в узле — ложь (false label, fl)
- Метка-знак (sign) (подробнее см. далее)
Нумерация вершин выполняется в произвольном порядке, единственным условием является уникальность номеров узлов.
Разметка дерева производится следующим образом:
- В tl указывается номер вершины, в который делается переход или truelab, если данная вершина true
- В fl указывается номер вершины, в который делается переход или falselab, если данная вершина false
Sign указывает то, в каком случае можно прекратить вычисления текущего поддерева.
Для корня дерева tl=truelab, fl=falselab, sign=false.
Таким образом:
| Операнд | fl | tl | sign |
|---|---|---|---|
| Левый операнд OR'a | Номер правого операнда | tl родительского узла | true |
| Правый операнд OR'a | fl родительского узла | tl родительского узла | sign родительского узла |
| Левый операнд AND'a | fl родительского узла | Номер правого операнда | false |
| Правый операнд AND'a | fl родительского узла | tl родительского узла | sign родительского узла |
| Операнд NOT'a | tl родительского узла | fl родительского узла | отрицание sign родительского узла |
Пример
Разметить дерево, построенное для логического выражения not A or B and C and (B or not C).
Генерация кода
Машинные команды, используемы в сгенерированном коде:
- TST <boolean value> — проверка аргумента на истинность и установка флага, если аргумент ложен
- BNE <label> — переход по метке в случае, если флаг не установлен, то есть проверяенное при помощи TST условие истинно
- BEQ <label> — переход по метке в случае, если флаг установлен, то есть проверяенное при помощи TST условие ложно
Построение кода производится следующим образом:
- дерево обходится от корня, для AND и OR сначала обходится левое поддерево затем правое
- для каждой пройденной вершины печатается ее номер (метка)
- для листа A(номер, tl, fl, sign) печатается TST A
- если sign == true, печатается BNE tl
- если sign == false, печатается BEQ fl
Пример
Для рассмотренного выше выражения сгенерируется следующий код:
1:2:4: TST A
BEQ TRUELAB
3:5:7: TST B
BEQ FALSELAB
8: TST C
BEQ FALSELAB
6:9: TST B
BNE TRUELAB
10:11: TST C
BNE FALSELAB
TRUELAB:
FALSELAB:
Метод сопоставления образцов
Идея метода заключается в том, что для одного и того же участка программы может быть код сгенерирован различными способами, и, как следствие, можно добиться оптимизации по тому или иному параметру.
Постановка задачи
Имеется множество образцов, для каждого из которых определён кусок промежуточного представления, для которого он применим, вес и генерируемый код. Есть дерево промежуточного представления, представляющее собой фрагмент программы, для которой необходимо код сгенерировать. Целью является построение такого покрытия дерева промежуточного представления образцами, чтобы суммарный вес образцов был минимален.
Образцы - это ассемблерные команды и деревья разбора, которые им соответствуют. Про каждый образец известно время его выполнения (в тактах). С их помощью и будем генерировать оптимальный (по времени выполнения) код.
Примеры образцов
Построение промежуточного представления
Сначала строим дерево разбора для всего выражения.
Построение покрытия
Теперь для каждой вершины (перебираем их в порядке от листьев к корню) будем генерировать оптимальный код для ее поддерева. Для этого просто переберем все образцы, применимые в данной вершине. Время выполнения при использовании конкретного образца будет складываться из времени вычисления его аргументов (а оптимальный код для их вычисления мы уже знаем благодаря порядку обхода дерева) и времени выполнения самого образца. Из всех полученных вариантов выбираем лучший - он и будет оптимальным кодом для поддерева данной вершины. В корне дерева получим оптимальный код для всего выражения.
Генерация кода
Код для всех вершин выписывать не обязательно - достаточно записать минимальное необходимое время и образец, которым нужно воспользоваться. Все остальное из этого легко восстанавливается.
Регистров у нас в этих задачах бесконечное количестов, так что каждый раз можно использовать новый.
Построение РВ по ДКА
Построение НКА по праволинейной грамматике
Приведение грамматики
Для того чтобы преобразовать произвольную КС-грамматику к приведенному виду, необходимо выполнить следующие действия:
- удалить все бесплодные символы;
- удалить все недостижимые символы;
Удаление бесполезных символов
Вход: КС-грамматика G = (T, N, P, S).
Выход: КС-грамматика G’ = (T, N’, P’, S), не содержащая бесплодных символов, для которой L(G) = L(G’).
Метод:
Рекурсивно строим множества N0, N1, ...
- N0 = ∅, i = 1.
- Ni = {A | (A → α) ∈ P и α ∈ (Ni - 1 ∪ T)*} ∪ Ni-1.
- Если Ni ≠ Ni - 1, то i = i + 1 и переходим к шагу 2, иначе N’ = Ni; P’ состоит из правил множества P, содержащих только символы из N’ ∪ T; G’ = (T, N’, P’, S).
Пример
Удалить бесполезные символы у грамматики G({A, B, C, D, E, F, S}, {a, b, c, d, e, f, g}, P, S)
- S → AcDe | CaDbCe | SaCa | aCb | dFg
- A → SeAd | cSA
- B → CaBd | aDBc | BSCf | bfg
- C → Ebd | Seb | aAc | cfF
- D → fCE | ac | dEdAS | ε
- E → ESacD | aec | eFf
Решение
- N0 = ∅
- N1 = {B (B → bfg), D (D → ac), E (E → aec)}
- N2 = {B, D, E, C (C → Ebd)}
- N3 = {B, D, E, C, S (S → aCb)}
- N4 = {B, D, E, C, S} = N3
G'({B, C, D, E, S}, {a, b, c, d, e, f, g}, P', S)
- S → CaDbCe | SaCa | aCb
- B → CaBd | aDBc | BSCf | bfg
- C → Ebd | Seb
- D → fCE | ac | ε
- E → ESacD | aec
Удаление недостижимых символов
Вход: КС-грамматика G = (T, N, P, S)
Выход: КС-грамматика G’ = (T’, N’, P’, S), не содержащая недостижимых символов, для которой L(G) = L(G’).
Метод:
- V0 = {S}; i = 1.
- Vi = {x | x ∈ (T ∪ N), (A → αxβ) ∈ P и A ∈ Vi - 1} ∪ Vi-1.
- Если Vi ≠ Vi - 1, то i = i + 1 и переходим к шагу 2, иначе N’ = Vi ∩ N; T’ = Vi ∩ T; P’ состоит из правил множества P, содержащих только символы из Vi; G’ = (T’, N’, P’, S).
Определение: КС-грамматика G называется приведенной, если в ней нет недостижимых и бесплодных символов.
Пример
Удалить недостижимые символы у грамматики G'({B, C, D, E, S}, {a, b, c, d, e, f, g}, P', S)
- S → CaDbCe | SaCa | aCb
- B → CaBd | aDBc | BSCf | bfg
- C → Ebd | Seb
- D → fCE | ac | ε
- E → ESacD | aec
Решение
- V0 = {S}
- V1 = {S, C (S → CaDbCe), D (S → CaDbCe), a (S → CaDbCe), b (S → CaDbCe), e (S → CaDbCe)}
- V2 = {S, C, D, a, b, e, E (C → Ebd), d (C → Ebd), f (D → fCE)}
- V3 = {S, C, D, E, a, b, d, e, f, c (E → ESacD)}
- V4 = {S, C, D, E, a, b, d, e, f, c} = V3
G''({C, D, E, S}, {a, b, c, d, e, f}, P'', S)
- S → CaDbCe | SaCa | aCb
- C → Ebd | Seb
- D → fCE | ac | ε
- E → ESacD | aec